2022-ICLR-Sample Selection with Uncertainty of Losses for Learning with Noisy Labels

Introduction

2022今時点でのNoisy Labelは二つの方向性がある。ノイズ変換行列と、正しそうなサンプルを選ぶというもの。前者は実データがインスタンス依存である、条件が複雑なのもあって性能が頭打ちしているように見えている。本論文は後者のSample Selectionについて論じる。

ではどのような基準でSample Selectionするかが問題。Memorization Effectにより、DNNはまずは本質的なパターンを覚えたうえで、ノイズに過学習していくので、本質的なパターンを覚えた時に小さい損失を持つサンプルがCleanなラベルを持ってると考えられそう=Small Loss Trick。これが現行の主流の考え方。

しかし、損失が小さいものをただ選ぶだけだと決定性になってよくないよね。一度間違った方向性を選ぶとこの傾向がずっと拡大してしまう。また、たとえCleanでも大きな損失を持つ一部のサンプルが学習されないという問題がある。

一例として、Imbalanced Dataの学習をするとき、損失が大きい理由として、同じカテゴリのサンプルを一杯学習してないからという原因もあるわけで。

これを解消するために、不確定性をSample Selectionに導入した手法を提案する。

Method

問題設定

$k$ クラス分類であり、入力空間 $\mathcal{X}$ と出力空間 $\mathcal{Y}$ であるとする。
学習器は $f : \mathcal{X} \to \mathbb{R}^k$ であり、出力するのはそれぞれのクラスについての特徴。 $i$ 回目のイテレーションでの学習器パラメタを $\mathbf{w}_i$ とする。
損失関数は $l: \mathbb{R}^k \to \mathcal{Y} \to \mathbb{R}$ として、特徴を受け取って損失を計算する。この損失を最小化していくことが目標である。同様に $i$ 回目のイテレーションでの損失を $l_i$ とする。
- 毎回の損失 $l_i$ をすべて含んだ集合 $L_t = \{ l_1, \cdots, l_t \}$ を考える。
この論文では、 $L_t$ がマルコフ過程に従うと仮定する。

Extended Time Intervals

有限の訓練時間を持つとき、ノイズが多いクラス事後推定における不安定性の問題にうまく対処できないらしい。推定の最初で間違ったのを選ぶとまずい問題なのかな？

1つの考えとして、 $\mu = \frac{1}{t} \sum_{i=1}^t l_i$ と平均を取ることで、過去の損失を利用した情報を得る。より頻繁に各epochの平均を取る方が望ましい。

提案手法(Robust Mean Estimation and Conservative Search)

平均を取るという手法を拡張する。Soft Truncation, Hard Truncationの2つを提案する。truncation=切り捨て。どれを使うかはいくつかの仮定に基づく統計的検定によって決まるらしい。

Soft Truncationでは、外れ値に強く反応しないようにした写像による変換で解決させる。Hard Truncationでは、外れ値を排除したあとに平均を取る。

Soft Truncation

次のように平均っぽいものをとる。

\psi (X) = \log (1 + X + X^2 / 2), X \geq 0 \\ \mu_s = \frac{1}{t} \sum_{i=1}^t \psi(l_i)

指数関数のマクローリン展開を二乗の項までにして打ち切っている。これによって、極端な外れ値による影響を小さくすることができる。

Hard Truncation

$L_t$ の中でKNNアルゴリズムを使うことによって、 $t_o$ 個の外れ値検出ができる。具体的に $t_o$ がいくつかはアルゴリズムから自動的に検出される。他の検出アルゴリズムでも問題ないが、計算コストはKNNが一番低い。

検出した外れ値を $L_t$ から除外した集合を $L_{t-t_o}$ とする。そして、それの平均を取ることが、Hard Truncation。

\mu_h = \frac{1}{t = t_o} \sum_{l_i \in L_{t-t_o} }l_i

Soft Truncation & Hard Truncationの集中不等式

Soft Truncationに対しては以下の集中不等式がある。

Hard Truncationに対しては以下の集中不等式がある。

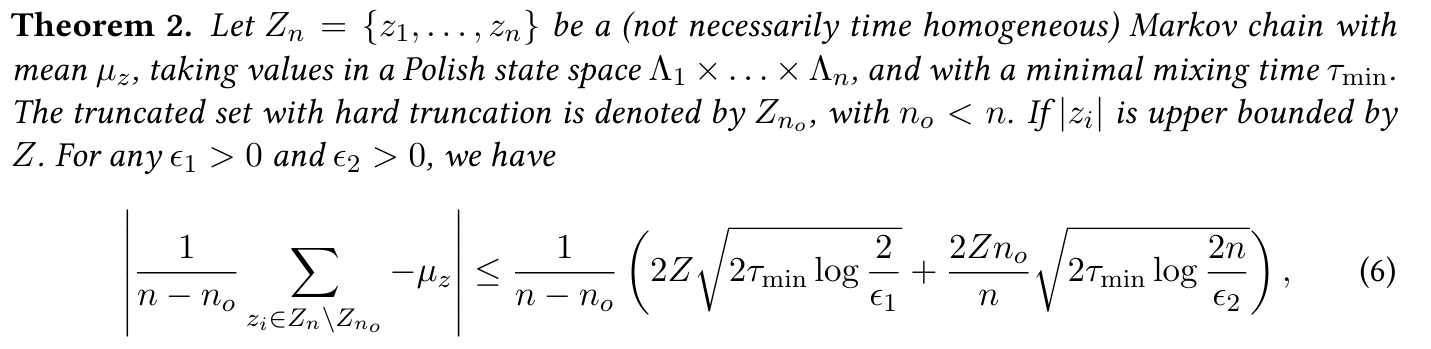
なんだかよくわからないが、訓練の損失上界を $L$ としている。

保守的な探索と選択基準

上の集中不等式を用いた、保守的な探索をするらしい。気持ちとしては、集中不等式の上界をそのまま使うので、かなり確実なサンプル以外は選ばない、ということ。

今まで $t$ 回のイテレーションで、あるサンプルが $n_t$ 回選ばれたとする。ここで、 $\epsilon = 1/(2t)$ として、Soft Trunctionを考えると、 $1 - 1/t$ 以上の確率で、まさにあの式が成り立つ。この時、損失の基準を

l_s^* = \mu_s - \frac{\sigma^2 (t + \frac{\sigma^2 \log (2t)}{t^2})}{n_t - \sigma^2}

として、small loss trickを駆使すれば、ちょうど集中不等式に含まれない部分を使わない、という基準にすることができる。

同様に、Hard Trunctionでは、 $\epsilon_1 = \epsilon_2 = 1/(2t)$ とすることによって、以下のよう閾値を設ける。

l_h^* = \mu_h - \frac{2 \sqrt{2\tau_{\min}} L (t + \sqrt{2} t_o)}{(t - t_o) \sqrt{t}}\sqrt{\frac{\log (4t)}{n_t}}

imbalanceな学習で、あまり訓練中で選択されなかった例は $n_t << t$ が成り立つ。その結果、分母の部分で上限が大きく増えることになる。なので、すべての訓練損失の平均を取るのではなく、固定長(XXepochごとに)ごとに平均をとる。こうすることで、全体の傾向をつかめる。

$l_s^*, l_h^*$ については、 $n_t$ が少ないと値は多く引かれて、小さくなる。小さい方が良いらしいがなぜなんだ？

選択基準（7）および（8）については、二つの項から構成されており、一つの項にはマイナス記号が付いています。式（7）（または式（8））の第一項は小さい損失の例の不確実性を減らすためで、ここではトレーニング損失に堅牢な平均推定を使用します。第二項、すなわち統計的信頼区間は、ネットワークに選択された回数が少ない例（小さいntを持つ）を選ぶことを奨励します。これら二つの項はσ^2またはτminで制約されバランスを取っています。損失の基本的な分布に強い仮定を導入することを避けるため【8】、ノイズがある検証セットでσとτminを調整します。誤ってラベル付けされたデータについては、モデルはそれらに高い不確実性を持っています（つまり、小さいnt）そしてそれらを選びがちですが、誤ってラベル付けされたデータへの過剰適合は有害です。また、議論されているように、誤ってラベル付けされたデータとクリーンなデータを区別することは、場合によっては非常に困難です。したがって、保守的な方法で基本的なクリーンなデータを探すべきです。本論文では、σとτminを小さな値で初期化します。この方法は誤ってラベル付けされたデータの悪影響を減らし、同時に大きな損失を持つクリーンな例を選択することができ、これが一般化を助けます。より多くの評価は第3節で提示されます。

アルゴリズム

Co-Teachingを行う。

$\bar{S}_1, \bar{S}_2$ (4, 5ステップ)では、さきほど決めた $l^*$ の閾値に従って、損失が小さいものを選択している。 $R(T)$ でどれほどの割合を選ぶかを決めており、内実は $l^*$ の閾値で判断している。

最初は $R(T)$ は大きく=大量のサンプルで学習するが、最終的には小さくなって一部のサンプルで学習するということになる。これはMemorization Effectによって、はじめは大量にやって簡単な特徴をつかんでもらい、細部の記憶をするときはCleanだと思われるラベルだけを使うというものである。